In my previous post, I made the insinuation that election commentators had no idea who would win the election. Broadly this is true, but of course, when you are paid to write opinion, you have to say more than this. The biggest factor they talk about is UKIP. At the start of January, it was generally thought that UKIP would take most votes from the Conservatives, but would also still take some votes from labour. However, a rise in support for UKIP would favour Labour as the winning party, a decline in votes for UKIP would favour the conservatives.
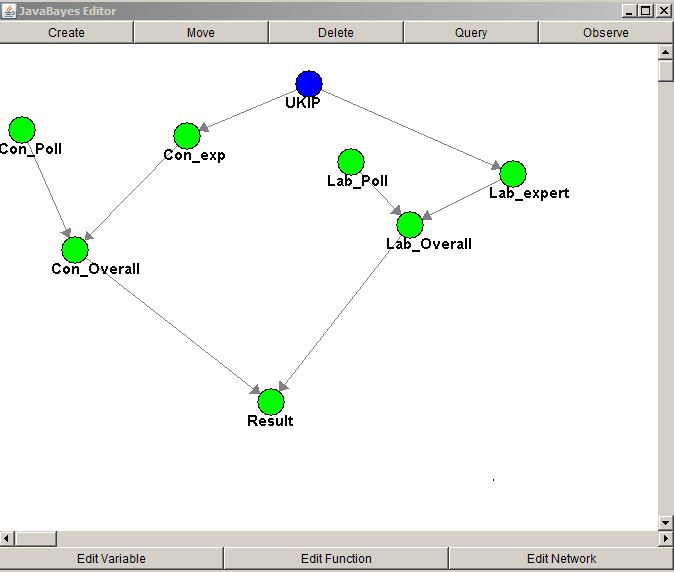
In this case, we have a simple interaction – UKIP influences labour and conservative (we don’t really need to consider the reciprocal, it’s unlikely UKIP will get the most votes, even if they get a lot). Bayesian belief networks handle these simple interactions well. We have a new structure for the network:
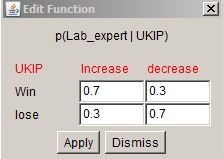
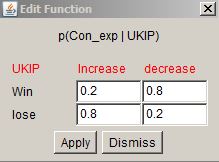
And some new functions – quite simple, what will happen to expert opinion should UKIP votes increase (or decrease). Everything else is the same.
In the network, the UKIP node is blue. The reason for that is that this can be ‘observed’. Being observed gives the node a probability of 1 (of increasing – OR of decreasing). Of course, we can’t be that certain, but we can use this to help predict what might happen, depending on what happens to UKIP.
Fundamentally, if we don’t know what happens to UKIP, then the pollsters have no idea who will win. We get the same probabilities as before (62% likely for a labour win). However, if the UKIP vote decreases (let’s assume the highly unlikely event of Nigel Farage saying something offensive in the next 4 and a half months….. ) then we observe that the UKIP vote goes down and… it’s now only 53% likely that Labour will get the most votes.
Simple Bayesian belief networks are fine for these simple interactions – but let’s go back to the football. Only four teams can qualify for Europe, so if one becomes more likely, this should effect the chances of the others. Simple Bayesian networks don’t cope well with this – but in what is likely to be the final part of these blogs, I’ll show how this can be overcome and we can incorporate interaction, data and opinion to make some final predictions.